Projects

Democratizing Uncertainty Quantification

Background

Uncertainty quantification (UQ) for advanced mathematical models can offer valuable insights in scientific projects.

However, widespread adoption of advanced UQ methods is held back by technical issues when integrating UQ and numerical models. In addition, there is a lack of reproducible benchmark problems, which are needed to drive future UQ development.

Contribution

I started the UM-Bridge project that facilitates straightforward application of numerous advanced UQ codes to any numerical simulation tool. UM-Bridge enables scaling up UQ applications to cloud and supercomputers, and is the technical foundation for the first library of UQ benchmark problems.

Outcome

UM-Bridge has facilitated numerous challenging academic UQ applications, ranging from prototypes to large-scale cloud computing. Early industry adoption is in progress.

Participants across more than 10 international institutions are contributing to the UM-Bridge benchmark library.

Uncertainty Quantification for Large-Scale Models

Background

Uncertainties in data, for example due to measurement errors, are ubiquitous. Quantifying their effect on model predictions and inferences is a major challenge, with simple approaches often necessitating excessive numbers of simulation runs.

Contribution

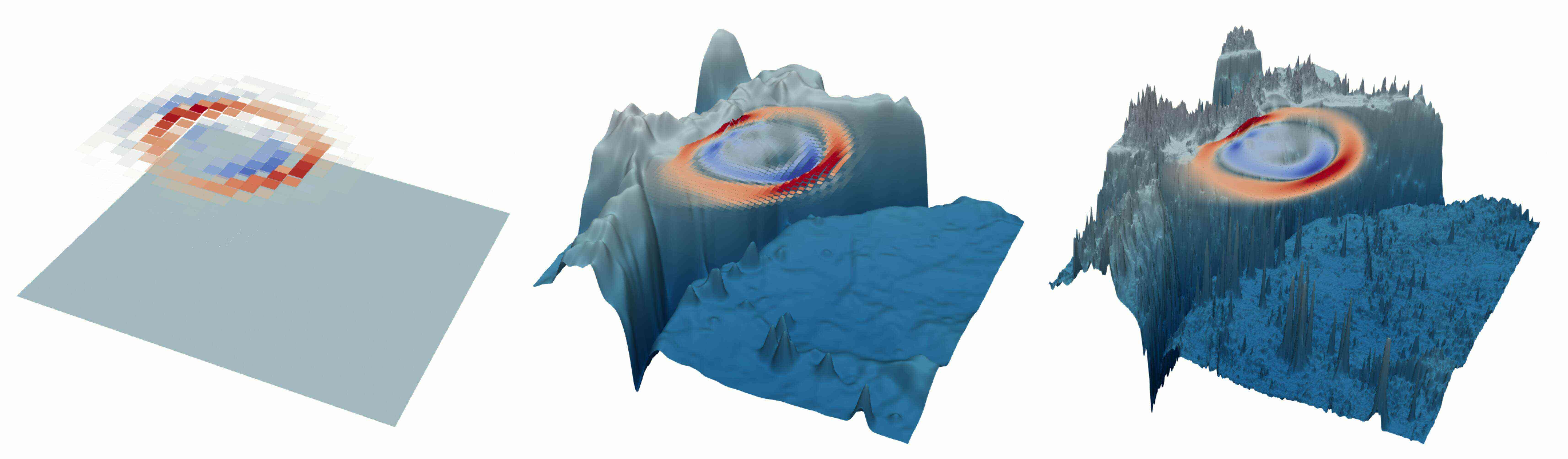
Tsunami model hierarchy

The key contribution of my PhD project is a massively parallelized version of Multilevel Markov chain Monte Carlo (MLMCMC). It was accepted into the MIT Uncertainty Quantification library.

Outcome

Using this method, we could solve a Bayesian inference problem on a challenging Tsunami model on ~3,500 processor cores of SuperMUC-NG at Leibniz supercomputing center.

Scalable Solver for Multiscale PDE Models

Background

Mathematical models are hard to solve numerically when multiple physical scales interact.

This is the case with carbon fiber composites, limiting industry standard solvers to relatively small scale simulations.

Contribution

As part of CerTest, I developed the first highly scalable implementation of GenEO. This mathematical method automatically identifies and eliminates critical components of the solution space, thus retaining the solver’s efficiency.

My GenEO implementation can be applied to a large class of PDE problems and was accepted into the DUNE numerics framework.

Outcome

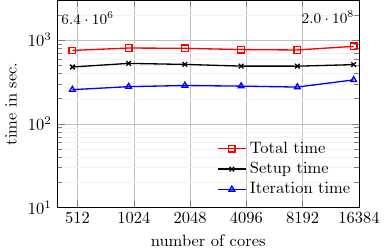
GenEO weak scaling

We could successfully simulate large composite aircraft structures on up to ~16,000 processor cores of the ARCHER UK national supercomputer, exceeding industry standard by a factor of ~1000.